 Graph learning with ENCO
Graph learning with ENCOAbstract
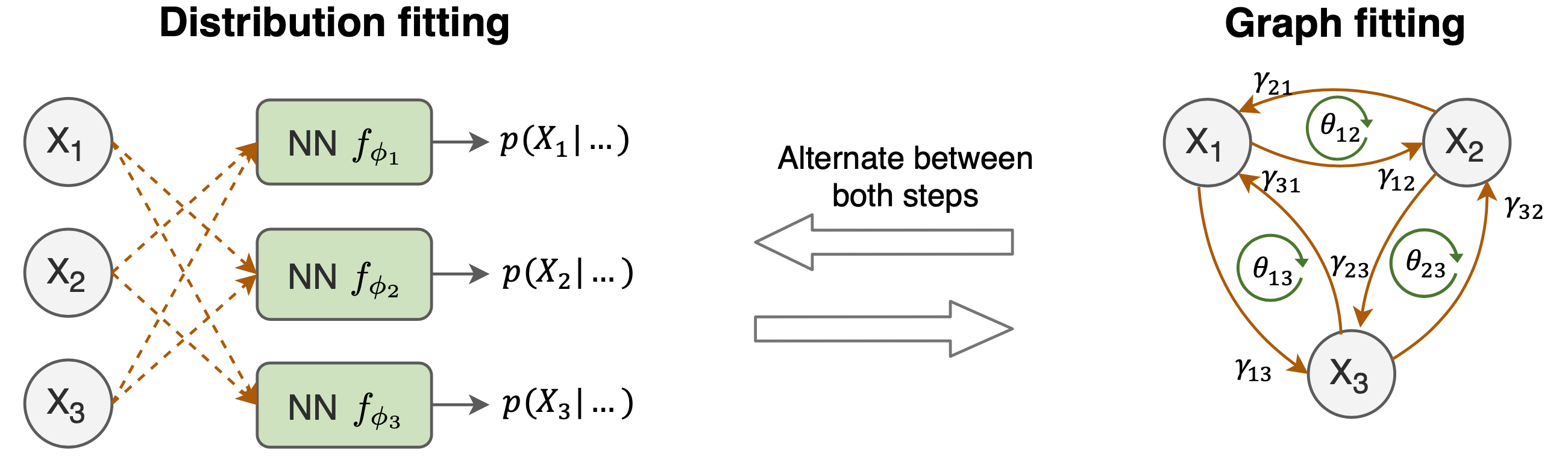
Learning the structure of a causal graphical model using both observational and interventional data is a fundamental problem in many scientific fields. A promising direction is continuous optimization for score-based methods, which efficiently learns the causal graph in a data-driven manner. However, to date, those methods require constrained optimization to enforce acyclicity or lack convergence guarantees. In this paper, we present ENCO, an efficient structure learning method for directed, acyclic causal graph leveraging observational and interventional data. ENCO formulates the graph search as an optimization of independent edge likelihoods, with the edge orientation being modeled as a separate parameter. Consequently, we can provide convergence guarantees of ENCO under mild conditions without constraining the score function with respect to acyclicity. In experiments, we show that ENCO can efficiently recover graphs with hundreds of nodes, an order of magnitude larger than what was previously possible.
The work has been published at ICLR 2022, and a shorter version accepted as a workshop paper + contributed talk to the 8th Causal Inference workshop at UAI 2021 can be found here.